最適化ツール
最適化ツール
最適化ツールは、行列、手動、ファイルの入力モードを使用して、線形計画法(LP)、混合整数線形計画法(MILP)、二次計画法(QP)最適化問題を解決します。
このツールはRツールを使用します。[オプション] > [予測ツールのダウンロード]に移動し、[Alteryxダウンロードとライセンス]ポータルにサインインして、Rツールで使用するパッケージとRツールをインストールします。詳細については、予測ツールのダウンロードと使用を参照してください。
最適化とは何ですか?
最適化は、サプライチェーン、輸送、金融サービス、小売、電気通信、エネルギーなど、多くの業界で幅広く適用されています。アプリケーション分野には、サプライチェーンの最適化、品揃えの最適化、ポートフォリオの最適化、労働力のスケジューリング、スポーツのスケジューリングなどがあります。
最適化問題は通常、目的関数(第1の方程式)、制約のセット(第2の方程式)、型(連続、整数、2進)の指定、決定変数(第3の方程式)の境界からなる、以下のような数学的形式になります。通常、基本的な制約、型、境界をすべて満たしながら、目的を最大化または最小化する決定変数の値を見つけることが目的です。
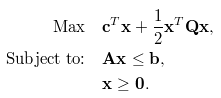
入力の接続
手動またはファイル入力モードでは、入力の必要はありません。行列入力モードの場合、入力OとAが必須ですが、BとQは任意です。入力Bのみが任意の場合もあります。行の制約を選択した場合のみ、入力Aで情報を指定できない場合があります。
Oアンカー: (行列入力モードで必須)この入力を使用して、決定変数の名前と目的関数の係数、オプションでその境界とタイプを指定します。
Rの機能により、フィールド名は大文字と小文字が区別されます。Designer 11.0以降では、フィールド名の柔軟性を高めるために[入力アンカーOのフィールドマッピングを表示]オプションを有効にできます。
変数(必須): 決定変数の名前の文字列。方程式のxに対応します。
係数(必須): 目的関数内の各決定変数の係数。cに対応します。
Ib (オプション): 決定変数の下限の数値。デフォルト値は0です。
ub (オプション): 決定変数の上限の数値。既定値はInf(正の無限大)です。
タイプ(オプション): 決定変数のタイプを表す文字列。C(連続)、B(バイナリ)、I(整数)のいずれかです。既定値はCです。
Aアンカー(行列入力モードで必須): この入力を使用して、方程式にAに対応する制約行列を指定します。マトリックスは、次の2つの異なる方法で編成できます。
密行列:
行の制約: 各行は制約に対応しています。
最初のフィールドには、オプションで制約的な名前を付けて各行の制約名を示すことができますが、残りのフィールド名はOで定義された決定変数に対応させる必要があります。
また、dirフィールドとrhsフィールドを含めて、B入力をA入力に結合できます。
dir: 制約の不等式の方向を示す文字列。これは>=、<=、==のいずれかです。
rhs: 不等式の右側のbに対応する数値。
変数フィールド(下の例ではx、y、z)は数値でなければなりません。
列の順序は、入力Oの行の順序と一致する必要があります。
例: 制約方程式がx + 2y + 3z <= 4とx + y >= 1の場合、これらはすべて入力Aに対する適した入力です。
制約フィールドの場合：
制約
x
y
z
1
c1
1
2
3
2
c2
1
1
0
制約フィールドなし：
x
y
z
1
1
2
3
2
1
1
0
dirとrhsを含む：
x
y
z
dir
rhs
1
1
2
3
<=
4
2
1
1
0
>=
1
行の変数: 各行は変数に対応しています。
最初のフィールドには変数の名前を付ける必要がありますが、残りのフィールド名は制約名に対応させる必要があります。これは、上記の方程式のA行列の転置に対応しています。
制約フィールド(以下の例ではc1とc2)は数値でなければなりません。
入力Oと入力Aの変数の順序は同じでなければなりません。
例: 以下は入力Aに適した入力です。
変数
c1
c2
1
x
1
1
2
y
2
1
3
z
3
0
Designer 11.0以降、「制約」や「変数」に他のフィールド名を使用できます。最適化ツールは、どのフィールドに制約があり、どのフィールドに変数が含まれているかをインテリジェントに示します。しかしながら、命名規則は依然として適しており、推奨されています。
スパース行列: 制約セットが大きい場合は、A行列をそのSLAMフォームで指定できます。i、j、vの3つの必須フィールドで構成され、iとjは行インデックスと列インデックスで、vは行列要素の非ゼロ値です。スパースマトリックモードでは、常に行の制約を前提とします。
Bアンカー(Aでまだ指定していない場合は必須): この入力を使用して、制約の名前、方向、右側を指定します。
制約(オプション): 制約の名前を示す文字列。
dir:: 制約の不等式の方向を示す文字列。これは>=、<=、==のいずれかです。
rhs: 不等式の右側のb.に対応する数値。
Qアンカー(オプション): この入力を使用して、二次計画法問題の目的関数の二次部分を指定します。これは、方程式のQに対応します。密マトリックスまたは疎マトリックスとして指定できます。
密行列: フィールド名は、Oで定義された決定変数名に対応する必要があります。
スパース行列: フィールド名はi、j、vで、iとjは行インデックスと列インデックス、vは関連する行列要素の非ゼロ値です。
入力モード
モデルを行列として選択
行列モードは、密または疎(スラム)をサポートします。入力OとAは行列入力モードで必須です。
問題タイプを選択:
線形プログラム: (既定)(LP)連続決定変数を持つ線形目標と線形制約。
混合整数プログラム: (MILP)連続決定変数とともにバイナリまたは整数の決定変数を持つ線形目標と線形制約。
二次計画法: (QP)連続決定変数を持つ二次目標と線形制約。
解法を選択:
Glpk: (既定)線形プログラムと混合整数線形プログラムの場合。
Symphony: 線形プログラムと混合整数プログラムの場合。通常、こちらの方がGlpk for MILPよりも優れています。
Quadprog: 二次計画法の場合。
目的を最大化しますか?: 目的関数を最大化する場合は、このオプションを有効にします。それ以外の場合、ツールは目的関数を最小化します。
入力アンカーA用の制約モードを選択: 詳細については、上記の「入力の接続」を参照してください。
密行列、行の制約(既定)
密行列、行の変数
スパース (SLAM) 行列
入力アンカーOのフィールドマッピングを表示(オプション): 入力Oでは、予約語の変数、係数、lb、ub、または入力テーブルのフィールド名にタイプが必要です。別のフィールド名を使用する場合、またはフィールド名に先頭または末尾の空白が含まれる場合は、エラーが発生します。このオプションを有効にすると、既存のフィールドを対応する変数、係数、lb、ub、タイプのフィールドにマッピングでき、フィールド名を変更するためにセレクトツールを使用した追加ステップは不要です。
モデルを手動で入力
このモードでは、目的と制約を直接指定できる相互作用的なインターフェースが提供されます。感度解析は、線形計画問題に使用できます。
問題タイプを選択:
線形プログラム: (LP)連続決定変数を持つ線形目標と線形制約。
混合整数プログラム: (MILP)連続決定変数とともにバイナリまたは整数の決定変数を持つ線形目標と線形制約。
二次計画法: (QP)連続決定変数を持つ二次目標と線形制約。
解法を選択: Glpk (線形プログラムと混合整数プログラムの場合)、Symphony (線形プログラムと混合整数プログラムの場合)、Quadprog (二次計画法の場合)。
目的を最大化しますか?: 最大化の問題である場合は、このオプションを有効にします。
変数リスト: 決定変数名のコンマ区切りリストを指定します。
目的: 最大化または最小化する目的関数を指定します。
制約: 制約を指定します。制約内のすべての変数が不等号/等号記号の左側にあるようにします。(例: 制約2x>=y+4の解法は失敗しますが、制約2x-y>=4は正常に実行されます。どちらの方程式も数学的には同じですが、2つ目の方程式が解法の要件を満たしています)
境界とタイプ: 境界とタイプを指定します。
ファイルからモデルを指定
このモードは、業界標準のモデルファイル入力をサポートします。
ファイルの種類を選択: CLPEX_LP、MathProg、MPS_Freeのいずれか。
解法を選択: Glpk (線形プログラムと混合整数プログラムの場合)、Symphony (線形プログラムと混合整数プログラムの場合)、Quadprog (二次計画法の場合)。
ファイルを選択: 最適化モデルファイルを指定します。
出力の表示
Iアンカー: この出力は、ソリューションの相互作用的なダッシュボードを指定します。
Dアンカー: この出力は、パイプで区切られた3つのテーブル(要約、変数、制約)で構成されます。ワークフローのアップストリームで使用して、レポートやダッシュボードを作成できます。
Sアンカー: これは、目的関数の最適値と決定変数を持つ1つのテーブルで構成されるシンプルなデータ出力です。バイナリ決定変数(0/1)のみで構成される問題の場合、このテーブルには1の値しか含まれません。