 Optimierung-Tool
Optimierung-Tool
Das Optimierung-Tool löst anhand des Matrix-, manuellen und Dateieingabemodus Probleme bei der Optimierung der linearen Programmierung (LP), der gemischt-ganzzahligen linearen Programmierung (Mixed Integer Linear Programming, MILP) und der quadratischen Programmierung (QP).
Dieses Tool verwendet das R-Tool. Gehen Sie zu Optionen > Prognose-Tools herunterladen und melden Sie sich beim Alteryx Downloads and Licenses-Portal an, um R und die vom R-Tool verwendeten Pakete zu installieren. Weitere Informationen finden Sie unter Prognose-Tools herunterladen und verwenden.
Was bedeutet Optimierung?
Die Optimierung findet zahlreiche Anwendungen in einer Vielzahl von Branchen, wie Lieferkette, Transport, Finanzdienstleistungen, Einzelhandel, Telekommunikation und Energie. Zu den Anwendungsbereichen gehören die Optimierung der Lieferkette, des Sortiments, des Portfolios, der Personaleinsatzplanung und der Planung von Sportveranstaltungen.
Ein Optimierungsproblem wird mathematisch in der Regel in der folgenden Form dargestellt, die aus einer Zielfunktion (1. Gleichung), einem Satz Nebenbedingungen (2. Gleichung) und einer Spezifizierung der Typen (stetig, ganzzahlig, binär) und Grenzen der Entscheidungsvariablen (3. Gleichung) besteht. Das Ziel besteht in der Regel darin, die Werte der Entscheidungsvariablen zu ermitteln, die das Ziel maximieren oder minimieren, während alle zugrunde liegenden Nebenbedingungen, Typen und Grenzen eingehalten werden.
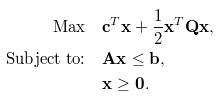
Eingaben verbinden
Für die manuelle oder die Dateieingabe werden keine Eingaben benötigt. Für den Matrixeingabemodus sind die Eingaben O und A erforderlich, B und Q sind jedoch optional. Eingabe B ist nur in einigen Fällen optional. Sie können die Informationen in Eingabe A nicht immer nur angeben, wenn Sie „Nebenbedingungen“ in Zeilen ausgewählt haben.
O-Anker: (Für Matrixeingabemodus erforderlich) Verwenden Sie diese Eingabe, um die Namen der Entscheidungsvariablen, deren Koeffizienten in der Zielfunktion und optional die Grenzen und Typen bereitzustellen.
Bedenken Sie, dass bei Feldnamen aufgrund der R-Funktion die Groß- und Kleinschreibung beachtet werden muss. Seit Designer 11.0 können Sie die Option „Feldzuordnung für Eingabeanker O anzeigen“ aktivieren, die für die Feldnamen mehr Flexibilität bietet.
variable (Pflichteingabe) Eine Zeichenfolge, Namen von Entscheidungsvariablen. Entspricht x in den Gleichungen.
coefficient (Pflichteingabe) Eine Zahl, Koeffizient der einzelnen Entscheidungsvariablen in der Zielfunktion. Entspricht c.
lb (Optional) Eine Zahl, untere Grenze der Entscheidungsvariablen. Der Standardwert ist 0.
ub (Optional) Eine Zahl, obere Grenze der Entscheidungsvariablen. Der Standardwert ist „Inf“ (positiv unendlich).
type (Optional) Ein Buchstabe, der Typ der Entscheidungsvariablen, der C (Stetig), B (Binär) oder I (Ganzzahl) lauten kann. Der Standardwert ist C.
A-Anker (Für Matrixeingabemodus erforderlich) Verwenden Sie diese Eingabe, um die Nebenbedingungsmatrix bereitzustellen, die in den Gleichungen A entspricht. Sie können die Matrix auf zwei verschiedene Weisen organisieren:
Vollbesetzte Matrix:
Nebenbedingungen in Zeilen: Jede Zeile entspricht einer Nebenbedingungen.
Das 1. Feld kann optional den Namen Nebenbedingung erhalten, um den Namen der Nebenbedingung in der jeweiligen Zeile anzuzeigen, während die übrigen Feldnamen mit den in O definierten Entscheidungsvariablen übereinstimmen müssen.
Darüber hinaus können Sie die Felder dir und rhs einfügen, die die Eingabe B in die Eingabe A aufnehmen.
dir: Eine Zeichenfolge, Richtung der Ungleichung der Nebenbedingung Diese muss >=, <= oder == lauten.
rhs: Eine Zahl, die rechte Seite der Ungleichung, entspricht b.
Die Variablenfelder (x, y, und z im Beispiel unten) müssen numerisch sein.
Die Reihenfolge der Spalten muss mit der Reihenfolge der Zeilen für die Eingabe O übereinstimmen.
Beispiel: Wenn Ihre Nebenbedingungsgleichungen x + 2y + 3z <= 4 and x + y >= 1, sind, sind diese sämtlichst zulässige Eingaben für die Eingabe A:
Mit Feld „Nebenbedingung“:
Nebenbedingung
x
y
z
1
c1
1
2
3
2
c2
1
1
0
Ohne Feld „Nebenbedingung“:
x
y
z
1
1
2
3
2
1
1
0
Mit dir und rhs:
x
y
z
dir
rhs
1
1
2
3
<=
4
2
1
1
0
>=
1
Variablen in Zeilen: Jede Zeile entspricht einer Variablen.
Das 1. Feld sollte den Namen Variable erhalten, während die übrigen Feldnamen den Namen der Nebenbedingungen entsprechen müssen. Beachten Sie, dass dies dem Transponieren der Matrix A in den obigen Gleichungen entspricht.
Die Nebenbedingungsfelder (c1 und c2 im Beispiel unten) müssen numerisch sein.
Die Reihenfolge der Variablen für Eingabe O und Eingabe Amuss identisch sein.
Beispiel: Dies ist eine zulässige Eingabe für Eingabe A:
Variable
c1
c2
1
x
1
1
2
y
2
1
3
z
3
0
Seit Designer 11.0 können Sie für „Nebenbedingung“ oder „Variable“ andere Feldnamen verwenden, das Optimierung-Tool leitet dann ab, welches Feld Nebenbedingungen und welches Variablen enthält. Die Namenskonvention wird jedoch weiterhin bevorzugt und empfohlen.
Dünnbesetzte Matrix: Für größere Sätze an Nebenbedingungen können Sie die Matrix A in der SLAM-Form angeben. Diese besteht aus den 3 Pflichtrfeldern i, j und v, wobei i und j Zeilen- und Spaltenindizes sind und v der Wert ungleich null des Matrixelements ist. Der Modus „Dünnbesetzte Matrix“ nimmt an, dass sich die Nebenbedingungen in Zeilen befinden.
B-Anker (Pflichtangabe, falls nicht bereits in A angegeben): Geben Sie hier den Namen, die Richtung und die rechte Seite der Nebenbedingungen an.
constraint (Optional) Eine Zeichenfolge, Name der Nebenbedingung.
dir: Eine Zeichenfolge, Richtung der Ungleichung der Nebenbedingung. Diese muss >=, <= oder == lauten.
rhs: Eine Zahl, die rechte Seite der Ungleichung, entspricht b.
Q-Anker (Optional) Verwenden Sie diese Eingabe, um für QP-Probleme den quadratischen Teil der Zielfunktion anzugeben. Entspricht Q in den Gleichungen. Sie können diese als vollbesetzte Matrix oder als dünnbesetzte Matrix angeben.
Vollbesetzte Matrix: Die Feldnamen sollten den in „O“ definierten Namen für Entscheidungsvariablen entsprechen.
Dünnbesetzte Matrix: Die Feldnamen lauten i, j, und v, wobei i und j Zeilen- und Spaltenindizes sind und v der Wert ungleich null des zugehörigen Matrixelements ist.
Eingabemodi
Modell als Matrizen auswählen
Der Matrixmodus unterstützt entweder vollbesetzte oder dünnbesetzte Matrizen. Für den Matrixeingabemodus werden die Eingaben O und A benötigt.
Problemtyp auswählen:
Lineares Programm: (Standard)(LP) Lineares Ziel und lineare Nebenbedingungen mit stetigen Entscheidungsvariablen.
Gemischt-ganzzahliges Programm: (MILP) Lineares Ziel und lineare Nebenbedingungen mit binären oder ganzzahligen Entscheidungsvariablen zusammen mit stetigen Entscheidungsvariablen.
Quadratisches Programm: (QP) Quadratisches Ziel und lineare Nebenbedingungen mit stetigen Entscheidungsvariablen.
Solver auswählen:
Glpk: (Standard) Für lineare Programme und gemischt-ganzzahlige lineare Programme.
Symphony: Für lineare Programme und gemischt-ganzzahlige Programme. Liefert für MILP in der Regel eine besserer Leistung als Glpk
Quadprog: Für Quadrac-Programme.
Ziel maximieren?: Aktivieren Sie diese Option, wenn Sie die Zielfunktion maximieren möchten. Andernfalls minimiert das Tool die Zielfunktion.
Restriktionsmodus für Eingabeanker A auswählen: Weitere Informationen finden Sie unter Eingaben verbinden oben.
Vollbesetzte Matrix, Nebenbedingungen in Zeilen (Standard)
Vollbesetzte Matrix, Variablen in Zeilen
Dünnbesetzte Matrix (SLAM)
Feldkartierung für Eingabeanker O anzeigen (optional): Eingabe O erfordert die reservierten Wörter variable, coefficient, lb, ub oder type für die Feldnamen der Eingabetabelle. Wenn Sie andere Feldnamen verwenden oder wenn den Feldnamen Leerzeichen voran- oder nachgestellt sind, tritt ein Fehler auf. Indem Sie diese Option aktivieren, können Sie Ihre vorhandenen Felder den entsprechenden Feldern variable, coefficient, lb, ub, und type zuordnen, ohne zusätzlich den Schritt auszuführen, die Feldnamen mit einem Auswählen-Tool zu ändern.
Modell manuell eingeben
Dieser Modus bietet eine interaktive Oberfläche, auf der Sie Ziele und Nebenbedingungen direkt angeben können. Für LP-Probleme ist eine Sensitivitätsanalyse verfügbar.
Problemtyp auswählen:
Lineares Programm: (LP) Lineares Ziel und lineare Nebenbedingungen mit stetigen Entscheidungsvariablen.
Gemischt-ganzzahliges Programm: (MILP) Lineares Ziel und lineare Nebenbedingungen mit binären oder ganzzahligen Entscheidungsvariablen zusammen mit stetigen Entscheidungsvariablen.
Quadratisches Programm: (QP) Quadratisches Ziel und lineare Nebenbedingungen mit stetigen Entscheidungsvariablen.
Solver auswählen: Glpk (für lineares Programm und gemischt-ganzzahliges Programm), Symphony (für lineares Programm und gemischt-ganzzahliges Programm) oder Quadprog (für quadratisches Programm).
Ziel maximieren?: Aktivieren Sie diese Option, wenn es sich um ein Maximierungsproblem handelt.
Variablenliste: Geben Sie die Namen von Entscheidungsvariablen als kommagetrennte Liste ein.
Ziel: Geben Sie eine Zielfunktion an, die maximiert oder minimiert werden soll.
Nebenbedingungen: Geben Sie die Nebenbedingungen an. Stellen Sie sicher, dass sich alle in der Nebenbedingung vorhandenen Variablen links vom Ungleich-/Gleich-Zeichen befinden. (z. B. tritt mit der Nebenbedingung 2x>=y+4 ein Solver-Fehler auf, mit der Nebenbedingung 2x-y>=4 wird der Solver jedoch erfolgreich ausgeführt. Auch wenn beide Gleichungen mathematisch äquivalent sind, erfüllt nur die zweite die Anforderungen des Solvers.)
Grenzen und Typen: Geben Sie die Grenzen und Typen an.
Modell über eine Datei festlegen
Dieser Modus unterstützt die Eingabe des Modells in einer Datei im Industriestandard.
Dateityp auswählen: CLPEX_LP, MathProg oder MPS_Free.
Solver auswählen: Glpk (für lineares Programm und gemischt-ganzzahliges Programm), Symphony (für lineares Programm und gemischt-ganzzahliges Programm) oder Quadprog (für quadratisches Programm).
Datei auswählen: Geben Sie eine Optimierungsmodelldatei an.
Ausgabe anzeigen
I-Anker: Diese Ausgabe bietet ein interaktives Dashboard der Lösung.
D-Anker: Diese Ausgabe besteht aus drei durch Trennlinien getrennten Tabellen: Zusammenfassung, Variablen und Nebenbedingungen. Diese können im weiteren Verlauf des Workflows verwendet werden, um Berichte und Dashboards zu erstellen.
S-Anker: Dies ist eine einfache Datenausgabe, die aus einer einzelnen Tabelle mit dem optimalen Wert der Zielfunktion und den Entscheidungsvariablen besteht. Für nur aus binären Entscheidungsvariablen (0/1) bestehende Probleme enthält diese Tabelle ausschließlich diejenigen mit dem Wert 1.
